이 시대에 데이터 분석은 매우 중요하며 데이터 분석 방법은 여러 가지로 발전했습니다. 카테고리를 골라서 앞으로 데이터 분석에 대한 시리즈를 쓸 예정이며 정의부터 실제 구현까지의 내용을 통해 쉽게 데이터 분석가가 될 수 있도록 하겠습니다. 첫 번째 데이터 분석 기법으로 boxplot부터 시작하겠습니다.
정당성
박스 플롯데이터의 분포를 시각적으로 나타내는 통계 차트 중 하나입니다. 숫자 데이터를 다룰 때 주로 사용되며 데이터의 중앙값, 최대값, 최소값, 사분위수를 표현할 수 있습니다.
- 범주별 분포를 비교할 때도 유용합니다.
- 데이터의 속성을 유추할 수 있는 대표 숫자 5개를 이미지로 표현할 수 있어 데이터의 속성을 바로 알 수 있음
- 이를 통해 데이터 활용 시 고려해야 할 사항을 파악하고 분석 방향을 설정할 수 있다.
박스 플롯직사각형 상자와 위스커로 구성됩니다. 직사각형 상자의 상단은 상위 25%(제3사분위수)를 나타내고 하단은 하위 25%(제1사분위수)를 나타냅니다. 상자 안팎의 수평선은 중앙값을 나타냅니다. 위스커는 상위 및 하위 25% 포인트를 제외한 전체 데이터 범위의 최대 및 최소 값을 나타냅니다. 그리고 상자 그림을 사용하면 데이터의 중심 경향과 분산을 한 눈에 보고 이상값을 식별할 수 있습니다. 이상값은 일반적인 데이터 분포에서 벗어나는 극단값입니다.
-
- 최소: 1사분위 – 1.5 IQR
- 1사분위수(Q1): 25% 위치
- 2사분위수(Q2): 50% 게재순위(중앙값을 의미)
- 3사분위수(Q3): 75% 위치
- 최대: 1.5 IQR + 3사분위에 위치
- IQR은 제3사분위수에서 제1사분위수를 뺀 사분위수 범위입니다.
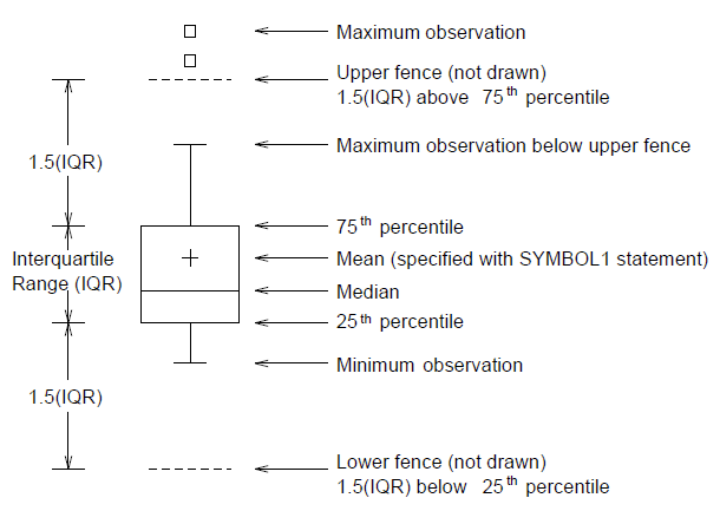
- 위의 예에서 상자 그림을 해석하면 중앙값이 약간 아래에 있기 때문에 분포가 오른쪽으로 약간 치우쳐 있다는 결론을 내릴 수 있습니다. 그리고 실제 최소값이 최소값 범위(제1 사분위수에서 IQR 1.5를 뺀 값)보다 훨씬 높기 때문에 데이터가 덜 왼쪽으로 흩어지는 것을 볼 수 있습니다. 그리고 최대값을 넘어서는 이상치의 존재로 판단하면 이 분포는 오른쪽 분포가 길다는 것을 알 수 있다.
- 99개의 데이터가 가장 작은 값부터 순서대로 있다고 가정하면 앞에서부터 25번째 값이 1사분위수이며 사분위수를 구하는 공식은 다음과 같습니다.
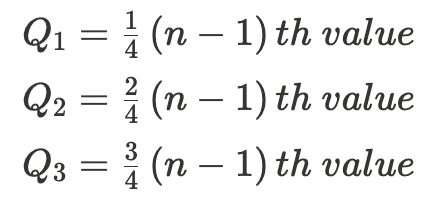
- dsf
z-score는 box plot을 그리기 위한 값을 계산할 때 데이터 포인트의 위치를 표준정규분포의 위치로 환산한 값이다. 모든 사람이 몇 백분위수에 속하는지 알아내는 데 사용할 수 있는 통계 기법입니다.
z 점수는 데이터 포인트가 평균에서 얼마나 떨어져 있는지를 나타내며 표준 편차의 배수로 계산됩니다. 즉, z-score가 0이면 데이터 포인트가 평균과 같은 위치에 있고, z-score가 양수이면 데이터 포인트가 평균보다 높게 위치하며, z-score가 음수이면 데이터가 점이 평균보다 낮습니다.
상자 그림에서 데이터 포인트가 상위 25%에서 하위 25% 범위에 있는 경우 z-점수는 (-0.67 ~ 0.67) 사이이며 이 범위를 벗어나는 데이터 포인트는 이상값으로 처리됩니다. 이렇게 하면 데이터에서 제거하거나 처리할 수 있는 이상값을 식별할 수 있습니다.
- 공식
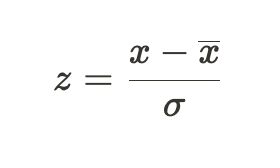
- (예시) 두 학생의 조건이 다음과 같을 때 각 z-score는 다음과 같은 의미를 갖는다.

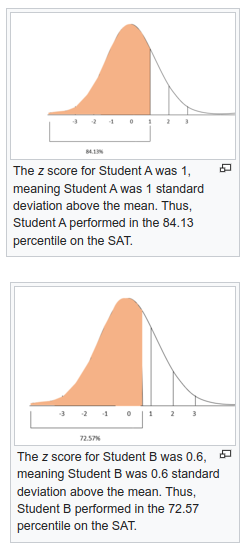
- 학생 A는 평균보다 1표준편차가 높습니다. 따라서 학생 A는 84.13에 있습니다. 백분위수
- 학생 B는 평균보다 0.6 표준 편차가 높습니다. 따라서 학생 B는 72.57에 있습니다. 백분위수
다음에는 boxplot을 실제로 구현할 것입니다. 데이터 분석은 파이썬으로 진행하는 것이 가장 빠르고 편리한 방법이니 파이썬으로 계속 해보자.


